Current Version: Profex 5.5.0 - Released May 17, 2025

Download files: Tutorial-RefMult.zip (0.8 MB)
Problem description
The sample contains α-TCP (α-Ca3(PO4)2) with two secondary phases β-TCP (β-Ca3(PO4)2) and β-CPP (β-Ca2P2O7). The powder was intensely milled in a high-energy ball mill as part of the production process. No further milling was therefore required for XRD sample preparation. Rietveld refinement was employed to quantify the amount of contaminates and the phase purity of α-TCP, respectively.
Creating the refinement control file
The raw file (150121-01.raw, Bruker RAW V4 format) was loaded into Profex, and by using the add phase dialog (+) a new refinement control file was created. The instrument configuration RMS-D8-ADS-15-LynxEyeXE was selected, and phases alphaTCP.str, betaTCP.str, and betaCPP.str were added. The pattern was clipped at 6° 2θ (WMIN=6) to remove the trace of the primary beam.
In the first run, all phases were refined with GEWICHT=SPHAR4 and B1=ANISO^0.01, and in addition, k2=0_0^0.0001 was refined for α-TCP to account for micro-strain introduced by thermal quenching and high-intensity milling. At this stage, the following phase quantities were obtained: α-TCP = 85.5 wt-%, β-CPP = 6.9 wt-%, β-TCP = 7.6 wt-%. The fit looked acceptable, but a problem with the β-TCP (2 -2 10) peak at 31°, and with the strong α-TCP peaks between 34° and 35° remained to be solved.

Detailed analysis of the peak shape revealed that there was a problem with the foot areas of strong α-TCP peaks. This was also the reason for the β-TCP (2 -2 10) peak drowning in the foot of the α-TCP peak to the left. No profile shape parameter (anisotropic k2, isotropic k1) was able to improve the fit.
Identifying the problem
It turned out that milling of the sample at the end of the production process was intense enough to create a fraction of much smaller crystallite size. The crystallite size of all three phases was therefore bimodal, and the profile shape parameters B1, k2, and k1 were not sufficient to describe the peak shape. Instead, for each of the three phases one highly crystalline contribution and one with severe peak broadening had to be refined to describe the overlap of sharp peaks with wide ones.
Using sub-phases
It could be assumed that the only difference between crystalline („coarse“) and nano-crystalline („fine“) fractions of the three phases was the peak broadening by crystallite size. No differences in unit cell dimension or atomic positions was expected. Rather than refining six phases independently (α-TCP coarse, α-TCP fine, β-TCP coarse, β-TCP fine, β-CPP coarse, β-CPP, fine), BGMN’s concept of sub-phases allows to only refine certain parameters independently, while coupling all other structural parameters. Here is how it’s done:
The following line was added to all three structure files to instruct BGMN to refine two sub-phases for each structure:
RefMult=2
Now two independent profile parameters B1, k2, and k1 could be refined for each phase. It was only done for B1, though, by modifying the profile parameters as follows in all three structure files:
PARAM=k2=0_0^0.0001 PARAM=B1[1]=0_0^0.003 PARAM=B1[2]=0.005_0.005^0.02
k2 was refined isotropically as usual (the same value for both sub-phases). B1 was refined separately for both sub-phases as B1[1] and B1[2]. The first one was varied between 0 and 0.003 for the coarse fraction, and the second one between 0.005 and 0.02 for the fine fraction.
Indeed the fit was drastically improved and could be considered almost perfect, also at the formerly problematic locations. However, the amounts of the two contamination phases were so low that there was a high risk for over-refining the data, as most peaks of both phases excessively overlapped with the much stronger α-TCP peaks. At the same time wrong micro-strain and crystallite size refinements could significantly bias refinement of phase quantities. It was therefore decided to couple both crystallite sizes B1[1] and B1[2], the micro-strain parameter k2, and the ratio of fine-to-coarse sub-phase p of β-TCP and β-CPP to the micro-strain, both crystallite sizes, and the coarse-to-fine ratio of the primary phase α-TCP to at least approximate the values in the secondary phases. Considering the preparation route of the sample and the similar hardness of all three phases, it was a sane assumption that:
- all three phases were broken down into a fine fraction to the same degree
- the coarse crystallite size of all three phases was similar
- the fine crystallite size was similar, too
- a similar amount of micro-strain was introduced in all three phases.
The parameters k2, B1[1], and B1[2] were refined globally in the refinement control file by adding the following lines:
PARAM[2]=B11=0_0^0.003 PARAM[3]=B12=0.005_0.005^0.02 PARAM[4]=k20=0_0^0.0001 PARAM[5]=p=0_0^1
p was the fraction of coarse phase. In all three structure files the profile parameters were refined as follows:
RP=4 k1=0 k2=k20 B1[1]=B11 B1[2]=B12 GEWICHT=SPHAR4
Additionally, the following lines were added to all three structure files to couple the coarse and fine fractions:
GEWICHT[1]=p*GEWICHT GEWICHT[2]=(1-p)*GEWICHT
Last but not least, to compute the correct phase quantities, two GOALs were used in each structure file, one for GEWICHT[1] (coarse fraction), and one for GEWICHT[2] (fine fraction):
GOAL:alphaTCPc=GEWICHT[1]*ifthenelse(ifdef(d),exp(my*d*3/4),1) GOAL:alphaTCPf=GEWICHT[2]*ifthenelse(ifdef(d),exp(my*d*3/4),1)
alphaTCPc was the coarse fraction, and alphaTCPf the fine one. This was done for betaTCPc, betaTCPf, betaCPPc, and betaCPPf, too. In the refinement control file, the quantities were calculated as follows to report total phase quantities:
sum=alphaTCPc+alphaTCPf+betaCPPc+betaCPPf+betaTCPc+betaTCPf GOAL[1]=(alphaTCPc+alphaTCPf)/sum GOAL[2]=(betaCPPc+betaCPPf)/sum GOAL[3]=(betaTCPc+betaTCPf)/sum
After the refinement the fit looked excellent:

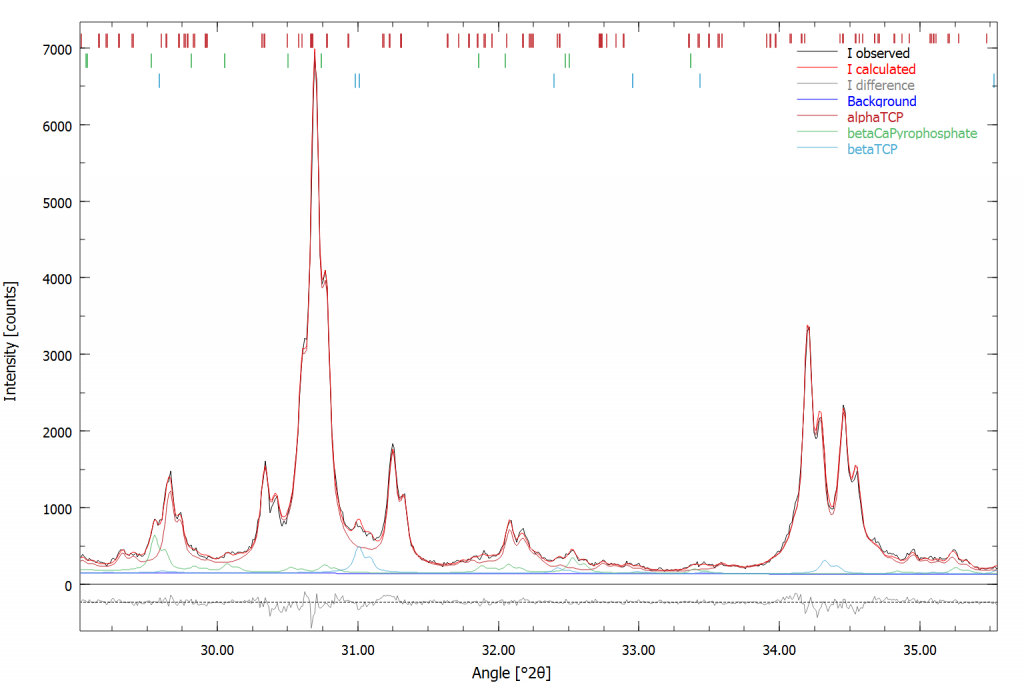
The phase composition was 89.1 wt-% α-TCP, 7.2 wt-% β-CPP, and 3.7 wt-% β-TCP. It shows that in the initial refinement the β-TCP quantity was over-estimated by factor 2. All phases contained 60% coarse and 40% fine fraction.
Summary
The following refinement strategy turned out to be successful:
- Sub-phases were used to refine two distinct
B1parameters for bimodal crystallite size distribution in all three phases - The
B1[1]parameters for large crystallites were coupled for all three phases and varied between 0 and 0.003 - The
B1[2]parameters for small crystallites were coupled for all three phases, too, and varied between 0.005 and 0.02 - One common
k2parameter was refined isotropically for all phases and sub-phases - One common parameter
pvarying between 0 and 1 was refined. It described the ratio between coarse and fine crystallite sub-phases
As a result a perfect fit was obtained without over-processing the data, peak shapes were described very accurately, and phase quantities seemed to be reliable.
Download files: Tutorial-RefMult.zip (0.8 MB)
α-TCP structure file (truncated):
PHASE=alphaTCP // 04-010-4348 Formula=Ca3_(PO4)2 // SpacegroupNo=14 HermannMauguin=P12_1/a1 // RefMult=2 PARAM=A=1.2887_1.2758^1.3016 PARAM=B=2.7280_2.7007^2.7553 PARAM=C=1.5219_1.5067^1.5371 // PARAM=BETA=126.20_124.94^127.46 // RP=4 k1=0 k2=k20 B1[1]=B11 B1[2]=B12 GEWICHT=SPHAR4 // GEWICHT[1]=p*GEWICHT // GEWICHT[2]=(1-p)*GEWICHT // GOAL=GrainSize(1,1,1) // GOAL:alphaTCPc=GEWICHT[1]*ifthenelse(ifdef(d),exp(my*d*3/4),1) // GOAL:alphaTCPf=GEWICHT[2]*ifthenelse(ifdef(d),exp(my*d*3/4),1) // E=CA Wyckoff=e x=0.3914 y=0.0260 z=0.0861 TDS=0.01229095 ...
β-TCP structure file (truncated):
PHASE=betaTCP // 04-008-8714 MineralName=Whitlockite // Formula=Ca3_(PO4)2 // SpacegroupNo=161 HermannMauguin=R3c // RefMult=2 PARAM=A=1.0439_1.0335^1.0543 PARAM=C=3.7375_3.7001^3.7749 // RP=4 k1=0 k2=k20 B1[1]=B11 B1[2]=B12 GEWICHT=SPHAR4 // GEWICHT[1]=p*GEWICHT // GEWICHT[2]=(1-p)*GEWICHT // GOAL=GrainSize(1,1,1) // GOAL:betaTCPc=GEWICHT[1]*ifthenelse(ifdef(d),exp(my*d*3/4),1) // GOAL:betaTCPf=GEWICHT[2]*ifthenelse(ifdef(d),exp(my*d*3/4),1) // E=CA Wyckoff=b x=-0.2766 y=-0.1421 z=0.1658 TDS=0.00686924 ...
β-CPP structure file (truncated):
PHASE=betaCaPyrophosphate // 04-009-3876 Formula=Ca2_P2_O7 // SpacegroupNo=76 HermannMauguin=P4_1 // RefMult=2 PARAM=A=0.6686_0.6619^0.6753 PARAM=C=2.4147_2.3906^2.4388 // RP=4 k1=0 k2=k20 B1[1]=B11 B1[2]=B12 GEWICHT=SPHAR4 // GEWICHT[1]=p*GEWICHT // GEWICHT[2]=(1-p)*GEWICHT // GOAL=GrainSize(1,1,1) // GOAL:betaCPPc=GEWICHT[1]*ifthenelse(ifdef(d),exp(my*d*3/4),1) // GOAL:betaCPPf=GEWICHT[2]*ifthenelse(ifdef(d),exp(my*d*3/4),1) // E=CA Wyckoff=a x=0.1374 y=0.2313 z=0.0000 TDS=0.00236081 ...
Refinement control file (complete):
% Theoretical instrumental function VERZERR=RMS-D8-ADS-15-LynxEyeXE.geq % Wavelength LAMBDA=CU % Phases STRUC[1]=alphaTCP.str STRUC[2]=betaCPP.str STRUC[3]=betaTCP.str % Measured data VAL[1]=150121-01.xy % Minimum Angle (2theta) WMIN=6 % Maximum Angle (2theta) % WMAX=60 % Result list output LIST=150121-01.lst % Peak list output OUTPUT=150121-01.par % Diagram output DIAGRAMM=150121-01.dia % Global parameters for zero point and sample displacement EPS1=0 PARAM[1]=EPS2=0_-0.01^0.01 alpha3ratio=0.018 betaratio=0.0158 NTHREADS=8 PROTOKOLL=Y SAVE=N PARAM[2]=B11=0_0^0.003 PARAM[3]=B12=0.005_0.005^0.02 PARAM[4]=k20=0_0^0.0001 PARAM[5]=p=0_0^1 sum=alphaTCPc+alphaTCPf+betaCPPc+betaCPPf+betaTCPc+betaTCPf GOAL[1]=(alphaTCPc+alphaTCPf)/sum GOAL[2]=(betaCPPc+betaCPPf)/sum GOAL[3]=(betaTCPc+betaTCPf)/sum
Nicola Doebelin, January 2015
